Let us try to tackle the problem of Special Right Triangles and Pythagorean Triplets, today. The theory will be followed by suitable examples for special right triangles. As you must be aware, the Pythagorean Theorem is one of the most used tools in geometry. Its three main features are:
1) One of the angles is a right angle
2) The sides which are adjacent to the right angle are termed as the base and perpendicular/height
3) The third side is known as the hypotenuse
For the figure given below, the hypotenuse is ‘c’, the base is ‘b’ and the perpendicular or height is ‘a’. As proposed by Pythagoras, the sum of square of sides adjacent to right angle is equal to the square of the third side, better known as the hypotenuse. Putting these words into equation form, we see:
a^2+ b^2=c^2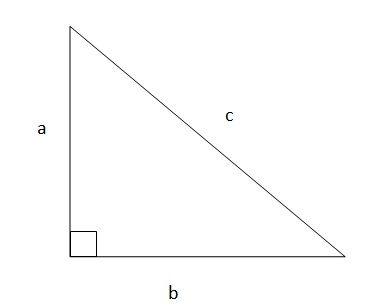
Two major takeaways from this theorem are:
a) It is applicable only to right angled triangles
b) The choice of base and perpendicular is irrelevant as far as the two sides adjacent to the right angled triangle are named.
Let us quickly see one application of Pythagorean Theorem before moving on to Special Right Triangles.
Example: John wants to visit his friend Ron’s house. He starts from his house and travels 3 km south before reaching a traffic signal. From there, he takes a 90 degree turn left and travels 4 km to reach Ron’s house. So how far is Ron’s house from John’s house?
Answer:
Let’s approach this question step by step
Step 1: Make a pictorial representation of the problem. Assume that John’s house is point A, the traffic signal is B, and Ron’s house is C.
Step 2: Mark the distances as shown. John’s house at point A to the Traffic Signal at B is 3 km, and from the Traffic Signal at B to Ron’s house at C is 4 km.
Step 3: The problem is to find the distance between Ron’s house and John’s house. As seen clearly from the pictorial representation, this can be solved by applying Pythagorean Theorem.
Step 4: Solving using the Pythagorean Theorem
AB^2+BC^2=AC^2
So, AC= sqrt(AB^2+BC^2)
AC= sqrt (3^2+4^2)
Therefore, distance AC= sqrt(25) = 5
Thus, the solution to the problem is: John’s house is 5 km from Ron’s house.
Pythagorean Triplets
One concept we can consider before moving forward is ‘Pythagorean Triplets’. As is clear from the name, these are sets of numbers that follow Pythagorean Theorem. Some examples are 3, 4, 5;
5, 12, 13;
8, 15, 17 and so on.
Quick tips
1) Knowledge of Pythagorean triplets in advance makes it easier to identify the number series and saves valuable time during exams.
2) If you multiply the triplet with any common number, the new triplet will also follow the Pythagorean rule.
Example 3, 4, 5 multiplied by two gives 6, 8, 10, which is also a Pythagorean triplet.
3) There are 16 such triplets under 100. I have given three examples above; try to learn the other 13 pairs too.
There are multiple ways in which Pythagorean Theorem can be applied, but some of the common applications in geometry are:
1) Using the standard form of the theorem to calculate distances and heights. This also has a good deal of applications in trigonometry.
2) The converse of theorem (i.e. if the sum of the square of two sides is equal to square of the third side, then it is a right angled triangle) also has a good variety of applications, especially in solving problems in geometry.
Special Right Triangles
Now let’s turn our attention to Special Right Triangles.
The first thing that comes to mind is: what is special about these triangles? The Special feature lies in the relationship of the sides or the angles. Let’s examine them one by one.
a) Side-based Special triangles
The special feature of side-based triangles comes from a ratio formation between the three sides. Pythagorean triplet is one such formulation.
3:4:5 ratio; 9:40:41 ratio
For example, suppose we have a problem like
The obvious way is to apply the Pythagoras theorem and calculate the third side, but there is a simpler way. On closer observation we can see that 21:28:? follows the 3:4:5 pattern with the original triplet multiplied by 7. Thus, the intended solution is 7*5=35
Hence knowledge of special triangle feature helps us to save valuable time by speeding up the pace of calculations.
The same property can be observed in the case of 9:40:41 and other similar triplets.
b) Angle-based special triangles
Two of the most useful cases are the 45:45:90 triangle and 30:60:90 triangle. In the case of the 45:45:90 triangle, the sides of the triangle would be in the ratio of n:n:n sqrt(2)
For example, if we have a problem to find out the length of the hypotenuse when the angles are 45:45:90 and the length of one side is 5 cm, then the length of the hypotenuse will be 5xsqrt(2) cm.
Quick tip: just a single bit of information (i.e. one of the angles of a right angled triangle is 45°) should be enough to tell that it is a 45:45:90 special triangle. This would help minimize the time spent calculating the lengths of the sides.
Case of 30:60:90 special triangle: these sides will follow the ratio of n:nxsqrt(3):2n for the two sides and the hypotenuse respectively.
Quick tip: If one of the angles of a right angled triangle is given as 30° or 60°, we can easily figure out the property that the sides of this triangle will follow the ratio of n:nxsqrt(3):2n
Importance of Pythagorean Theorem and Special Triangles
1) Lessens the pressure on students if they know the short cuts and properties of special triangles
2) Reduces the time taken to calculate complex triplets
3) Memorizing Pythagorean triplets under 100 is helpful in the exam.
About the Author

I am Atul Jose - the Founding Consultant at F1GMAT.
Over the past 15 years, I have helped MBA applicants gain admissions to Harvard, Stanford, Wharton, MIT, Chicago Booth, Kellogg, Columbia, Haas, Yale, NYU Stern, Ross, Duke Fuqua, Darden, Tuck, IMD, London Business School, INSEAD, IE, IESE, HEC Paris, McCombs, Tepper, and schools in the top 30 global MBA ranking.
I offer end-to-end Admissions Consulting and editing services – Career Planning, Application Essay Editing & Review, Recommendation Letter Editing, Interview Prep, assistance in finding funds and Scholarship Essay & Cover letter editing. See my Full Bio.
I am also the Author of the Winning MBA Essay Guide, covering 16+ top MBA programs with 240+ Sample Essays that I have updated every year since 2013 (11+ years. Phew!!)
I am an Admissions consultant who writes and edits Essays every year. And it is not easy to write good essays.
Contact me for any questions about MBA or Master's application. I would be happy to answer them all