Triangle Types and Similar Triangles

A triangle is a closed figure formed by three straight lines provided the sum of angles formed between the lines is 180 degrees. There are six types of triangles

• Isosceles Triangle: A triangle with two sides of equal length and corresponding angles of equal measure.

Example: Triangle with the angles 30°, 30° and 120°.

• Equilateral Triangle: A triangle that has all three sides of equal length and all three angles of equal measure. As the sum of the three angles must equal 180°, each angle equals 60° in an equilateral triangle.

• Scalene Triangle: If all the three sides of the triangle are of different size, then it is a scalene triangle.

Example: A triangle with sides 3cm, 4cm and 5cm is scalene.

• Right Triangle: A triangle that has one 90° angle. •    Acute Triangle: A triangle with all angles less than 90°.   

Example: A triangle formed with angles 50°, 60° and 70° is an acute triangle

• Obtuse Triangle: An obtuse triangle is a triangle with one angle greater than 90° o  

Example: Triangle with angles 30°, 30° and 120°.

Commonly used Terms

Altitude: The perpendicular distance from the base to the opposite vertex.

Base: We can take any side of the triangle as the base, for the purposes of further calculation.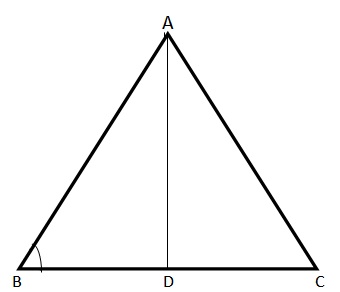



Vertex: Angles of triangles are called vertices.

Any one of AB, BC or AC could be taken as the base. In this case, AD is the Altitude, and BC is the base. Angle A, Angle B and Angle C are the vertices of the triangle.

Similar triangles

Similar triangles have the same shape, but not necessarily the same size.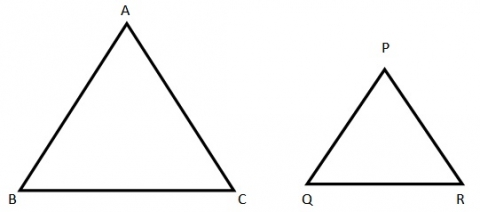



The similarity of triangles is based on one of the following three scenarios:

SSS Similarity: If each pair of corresponding sides has the same ratio, then the triangles are said to be similar.

So in the above figure, If AB/PQ = BC/QR = AC/PR, then the triangles are said to be similar, and written as ABC ~ PQR

AAA Similarity: If the corresponding angles of the given triangles are of the same measurement, then the triangles are said to be of AAA similarity.


So in the above figure if Angle A = Angle P, Angle B = Angle Q and Angle C = Angle R, then the triangles are similar.

SAS Similarity: If two corresponding sides of the triangles are of the same ratio and the angles formed by these sides are of the same measurement, then the triangles are said to be of SAS similarity.

In the above figure, if Angle A = Angle P and AB/PQ = AC/PR, then the triangles are similar.

GMAT problems on Triangles

1) Given that two triangles ABC and PQR are similar. AB = 10cm, BC = 8cm, Angle A=Angle B=60°. PQ = 5cm, QR=4cm. Find PR and AC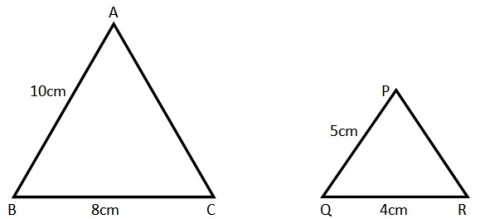



Solution: One needs to apply two concepts to get the values of PR and AC Given that both the triangles are similar

By following the SSS property, AB/AC = PQ/PR.

So 10cm/8cm = 5cm/PR

10/8 = 5/PR

5/4 = 5/PR

So PR = 4

Therefore PR = 4cm

Now we can find AC in two ways:

Method1: Given the data Angle A = Angle B = 60°. The triangle is isosceles; therefore the sides opposite the equal angles should also be equal. Hence BC = AC = 8cm

Method 2: We got PR=4cm. Again applying the rule for similar triangles AC/BC = PR/QR

AC/8cm = 4cm/4cm

AC/8 = 4/4

AC/ 8 = 1

AC = 1*8

AC = 8

Therefore AC = 8cm

Important points to remember

• The sum of any two sides of a triangle is always greater than the third side

• If we have the data given for two sides of a triangle, the length of the third side must lie between the difference and sum of the two given sides.

• The smallest side of the triangle will have the smallest angle opposite it. Similarly, the longest side of the triangle will have the largest angle opposite it.