The function g(x) is defined for integers x such that if x is even, g(x) = x/2 and if x is odd, g(x) = x + 5. Given that g(g(g(g(g(x))))) = 19, how many possible values for x would satisfy this equation?
A. 1
B. 5
C. 7
D. 8
E. 11
Explanation:
The easiest way to approach this problem is probably to work backwards, at least until we see a pattern.
With g(...) = 19, then we can consider which operation applied to (...). If it was x/2, then (...)= 38. 38 is even so that is fair. If it was x + 5, then (...) was 14. 14 is even, so that operation would not have been applied.
On paper, you could make a tree, with 19 as the root, and 38 as the first node.
Next consider 38. 38 could have come from 76/2 or 33 + 5. Two possibilities give us two nodes branching from 38:
19 -> 38 -> 76, 33.
We can now observe the pattern that with an odd number, it must have come from an even, but an even could come from either of two numbers.
Therefore our 76 will branch into 2 numbers, and the 33 into just one.
33 -> 66
76 -> 73, 152..
We can represent this as shown here: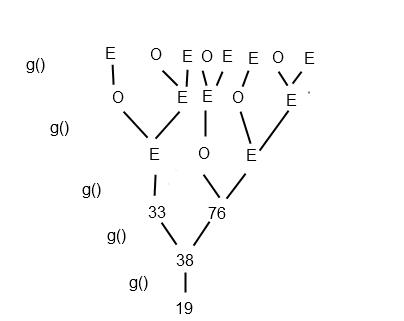
Counting at the base we see we have 8 original possibilities. Grockit,an online test prep game, is the smartest way to study for your test. It's adaptive, fun and finds the right teacher for you. Grockit’s analytic capabilities and adaptive technology identifies students' strengths and weaknesses, focusing the student's study time. Students can practice in adaptive solo games, play social learning games with peers, and work with experts that match their specific needs.
Grockit,an online test prep game, is the smartest way to study for your test. It's adaptive, fun and finds the right teacher for you. Grockit’s analytic capabilities and adaptive technology identifies students' strengths and weaknesses, focusing the student's study time. Students can practice in adaptive solo games, play social learning games with peers, and work with experts that match their specific needs.