Two sides of a right angled triangle are 15 cm and 17 cm. Find the length of the third side
I. 8 cm II. 32 cm III. Sqrt.514 cm IV. 514 cm
A) II only
B) I only
C) I & III only
D) II & III only
E) I, II & III
Solution
Apart from the math rules, we need to know how to look at these kinds of problems. We can see four options on the top: I, II, III and IV. Then we see five other options A, B, C, D and E.
In these types of problems, there will be the chance of more than one option for the given question. Therefore, the possible answers will be one or more among I, II, III and IV. Once we find them, we need to see the options A, B, C, D and E that give the option to choose one or more among I, II, III and IV. So our final answer that we need to mark in the test is among A, B, C, D and E.
Math Rules to know for solving this problem:
• Pythagoras theorem: The square of the hypotenuse is equal to the sum of the squares of other two sides.
So here (AC)^2 = (BC)^2 + (AB)^2
• The hypotenuse is the longest side of any right angled triangle.
• The sum of two sides is always greater than the third side.
Logic: Here the interesting fact is that we are given only the sides of the triangle, and the question did not mention if we can choose one as the hypotenuse or not. The sum of two given sides 15 and 17 is 32. The remaining side must therefore have a value of less than 32 cm. Here we can have two cases:
Case 1: The missing side (let us take it as X) is the hypotenuse and is greater than 17 cm and less than 32 cm.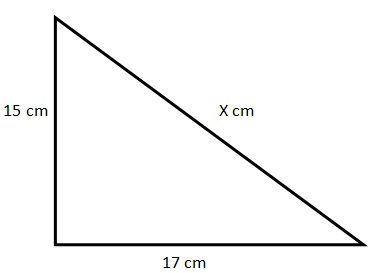 
Following Pythagoras theorem:
X^2 = 152 + 172
X^2 = 225 + 289
X^2 = 514
Taking the square root on both sides
X = sqrt. 514 cm
Therefore the third side is sqrt.514 cm.
Case 2: The missing side is not the hypotenuse, so 17 will be the hypotenuse in that case.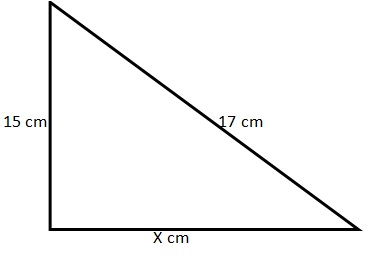
Again following Pythagoras theorem:
152 + X^2 = 172
225 + X^2 = 289
Subtracting X on both sides
X^2 = 289 – 225
X^2 = 64
Taking the square root on both sides
X = 8
Therefore the missing side is 8 cm.
So the third side can be sqrt. 514 cm or 8 cm. As seen in this problem there is more than one answer (I and III) for the given problem. Hence we need to see which option has both of them.
So the Answer will be Option C (I and III only)
About the Author 
GoGMAT, founded in 2009, is an adaptive GMAT preparation platform developed by the best instructors in the industry (with 740+ GMAT scores and strong teaching experience). GoGMAT team consists of high profile members, successful entrepreneurs, experts in educational field, top-notch business school alumni with successful track records as investment bankers and management consultants. Our GMAT experts, university professors and successful entrepreneurs, analyzed GMAT test algorithms for almost 12 months. We used their knowledge and skills as the basis to create one of the most efficient solutions in the world for GMAT preparation.
Disclaimer: The articles provided by GoGMAT are for informational purposes only and cannot be copied or redistributed without the written permission by GoGMAT. F1GMAT publishes guest posts by authors from all over the world. We do not accept any responsibility or liability for the information contained in the article or claims of copyright violation. However, we take immediate action when any copyright violations are reported. Report copyright violation