A. Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
B. Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
C. BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D. EACH statement ALONE is sufficient.
E. Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data are needed.
Explanation:
This question asks whether the information in one or both statements is sufficient to find a specific value. But we don't actually have to determine the value, just know that it can be determined.
(1) Quadratic equations have two solutions. However, sometimes those two solutions are identical with each other. If they are different, then solving this equation will lead to two possible values of x, and presumably also two possible values of f(x), so this would not be sufficient. But if they are the same, i.e. if there's really only one solution to this equation, then we would definitely know x, definitely know f(x), and definitely know f(x) - g(x). We have to plug in to find out how many solutions there are.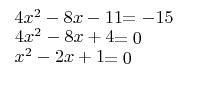
Either by factoring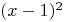 
or by using the quadratic equation 
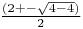, we see that this equation has a double root, 1, the two solutions are in fact identical. Since we know exactly what x is, we also can calculate f(x), and this is sufficient to calculate the value of f(x)-g(x). (33, but don't bother doing the calculation on the exam).
SUFFICIENT
(2) Here we are given a quadratic equation, which we could solve. Factoring, we'll find two roots: -7 and 1. So it would seem that this is not sufficient to know the value of f(x)-g(x).
However, don't despair too quickly. Although this isn't enough information to positively state the value of f(x) or g(x), it is enough to determine the value of f(x)-g(x). Subtracting the two equations, we get:
The credited response is D - each statement alone is sufficient.
Grockit, an online test prep game, is the smartest way to study for your test. It's adaptive, fun and finds the right teacher for you. Grockit’s analytic capabilities and adaptive technology identifies students' strengths and weaknesses, focusing the student's study time. Students can practice in adaptive solo games, play social learning games with peers, and work with experts that match their specific needs.